Angles and Triangles
|
Bisectors and Perpendicular Bisectors
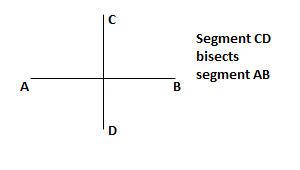
Two lines are perpendicular if they intersect each other to form two 90° angles. A line bisects a line segment if it divides the line segment into two equal lengths. The length of each of the new line segments is said to be "equidistant". A perpendicular bisector is a line that intersects a line segment to form two 90° angles and divides this line segment into two equal lengths. |
|
|
|
Intersecting Lines, Parallel Lines and Transversals
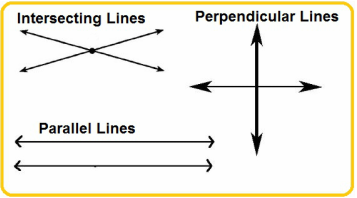
Two or more lines that meet at a point are called intersecting lines.
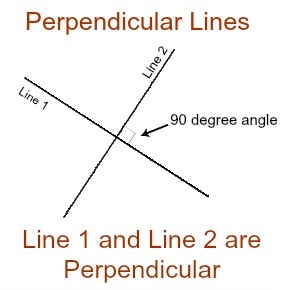
Two lines that intersect and form right angles are called perpendicular lines. The symbol ⊥ is used to denote perpendicular lines.
Two lines, both in the same plane, that never intersect are called parallel lines. Parallel lines remain the same distance apart at all times. The symbol // is used to denote parallel lines.
Two or more lines that meet at a point are called intersecting lines.
Two lines that intersect and form right angles are called perpendicular lines. The symbol ⊥ is used to denote perpendicular lines.
Two lines, both in the same plane, that never intersect are called parallel lines. Parallel lines remain the same distance apart at all times. The symbol // is used to denote parallel lines.
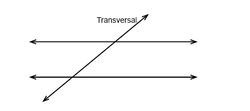
A transversal is two parallel lines intersected by a third line at an angle. The third line is referred to as the transversal line. When this line happens, several angles are created. You can use these angles to find the measurements of other angles.
Angles Formed by Intersecting Lines
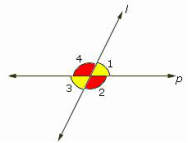
When lines intersect, there are several types of angles that are formed. Becoming familiar with these angles will greatly help your understanding of geometry. Firstly, some terms that will benefit your learning.
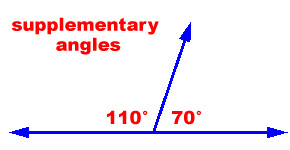
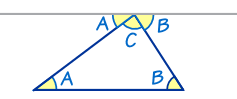
Adjacent Angles - Two angles are Adjacent when they have a common side and a common vertex (corner point) and don't overlap. In the diagram below (supplementary angles) angle 70 and angle 110 are adjacent to one another because they share a common side.
Straight Angles - A straight angle forms a "straight line" and is equal to 180 degrees.
In grade eight we will focus on two of these angle formations:
Angles Formed by Intersecting Lines
When lines intersect, there are several types of angles that are formed. Becoming familiar with these angles will greatly help your understanding of geometry. Firstly, some terms that will benefit your learning.
Adjacent Angles - Two angles are Adjacent when they have a common side and a common vertex (corner point) and don't overlap. In the diagram below (supplementary angles) angle 70 and angle 110 are adjacent to one another because they share a common side.
Straight Angles - A straight angle forms a "straight line" and is equal to 180 degrees.
In grade eight we will focus on two of these angle formations:
|
1) Supplementary Angles are pairs of angles that add up to 180 degrees. If you put two supplementary angle pieces together, you can draw a straight line across the top of the two angles. In essence, the two angles together make a half circle. Supplementary angles are not limited to adjacent lines as in the diagram to the right. They can be any two angles whose sum is equal to 180 degrees.
|
|
|
|
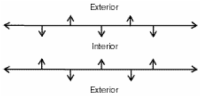
Angles Formed by Parallel Lines Cut by a Transversal
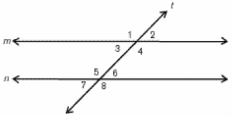
When two parallel lines are cut by a third line, the third line is called the transversal.
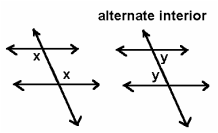
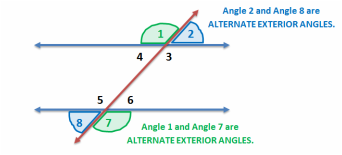
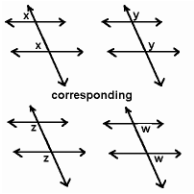
In the example to the right, eight angles are formed when parallel lines m and n are cut by a transversal line, t. There are 4 angles on the exterior of the figure (angles 1,2,7,8) and 4 angles on the interior of the figure (3,4,5,6).
Two special pairs of angles are formed in this arrangement (Alternate and Corresponding Angles):
In the example to the right, eight angles are formed when parallel lines m and n are cut by a transversal line, t. There are 4 angles on the exterior of the figure (angles 1,2,7,8) and 4 angles on the interior of the figure (3,4,5,6).
Two special pairs of angles are formed in this arrangement (Alternate and Corresponding Angles):
|
|
|
|
Proof
The top line (that touches the top of the triangle) is running parallel to the base of the triangle. So:
|
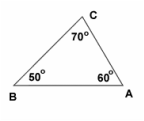
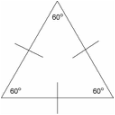
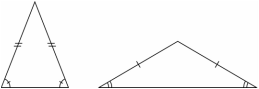
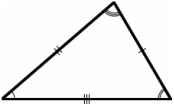
Types of Triangles
There are 3 special names given to triangles that tell how many sides (or angles) are equal. There may be 3, 2 or no equal sides/angles.
There are 3 special names given to triangles that tell how many sides (or angles) are equal. There may be 3, 2 or no equal sides/angles.
|
|
|
|
Angles in a Quadrilateral
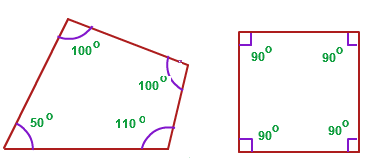
A quadrilateral has 4 straight sides. In a square the angles are all 90 degrees (see diagram on the far right). The interior angles of a square add up to 360 degrees. 90° + 90° + 90° + 90° = 360° However, if we tilt the edges slightly (see diagram to the immediate left) the sum of the angles is still 360 degrees. 100° + 100° + 110° + 50° = 360° Therefore, we can conclude that the Interior Angles of a Quadrilateral always add up to 360°. |
|
What About Polygons with more than Four Sides?
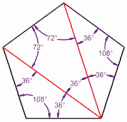
A pentagon has 5 sides, and can be made from three triangles (see diagram to the right). Therefore you can surmise that it's interior angles add up to 3 × 180° = 540° And if it is a regular pentagon (all angles are congruent), then each angle is 540° / 5 = 108° Therefore, we can conclude that the Interior Angles of a Pentagon add up to 540° (or 180° more than a quadrilateral). General Rule About Polygons and Angles
Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total |
|
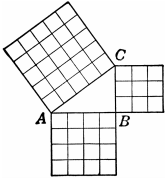
Exploring Right Triangles - The Pythagorean Theorem
Over 2000 years ago there was an amazing discovery made about triangles: When a triangle has a right angle (90°) and squares are made on each of the three sides, then the biggest square has the exact same area as the other two squares put together. (see diagram to the right) It is called the "Pythagorean Theorem" and can be written in the simple equation of: a² + b² = c² |