NUMBER RELATIONSHIPS
Day #1 Identifying Prime and Composite Numbers
Reminders:
The following video clips may help you to recall the concepts we discussed in class today:
Reminders:
- Prime Number has only two factors (one and itself).
- Composite Number has more than two factors.
- We can use Divisibility Rules to help us narrow down the possibilities of whether a number is prime or composite. The following is a list of the Divisibility Rules that will help you with your work today:
- 1. If number ends in 0 or 5 the number is divisible by 5,
2. Numbers ending in 0 are divisible by 2, 5 and 10,
3. Even numbers are divisible by 2
4. If the sum of the digits are divisible by 3, the number is divisible by 3
The following video clips may help you to recall the concepts we discussed in class today:
Day #2 Prime Factorization
Reminders:
- The goal of Prime Factorization is to write the number as a product of only prime numbers
- Factor trees allow us to arrive at Prime Factorization
The following clips will help you to review the concepts we discussed today in class:
| picture_001.jpg | |
| File Size: | 539 kb |
| File Type: | jpg |
Day #3 Common Factors and Common Multiples
Sept. Common Factors and Common Multiples activity pages 3-4
#1-2, 6-7
Reminders:
Sept. Common Factors and Common Multiples activity pages 3-4
#1-2, 6-7
Reminders:
- The Greatest Common Factor (GCF) is the greatest whole number that divides into two or more other whole numbers with no remainder. For example, 4 is the GCF of 8 and 12.
- An Upside Down Birthday Cake can be used to Find GCF (see the video below for helpful instructions)
- The Lowest Common Multiple (LCM) is the least whole number that has two or more given numbers as factors. For example, 12 is the LCM of 4 and 6.
- Venn Diagrams can be used to organize common and uncommon factors when considering numbers to identify both the GCF and the LCM. See the video below for helpful instructions on how to use this tool.
- The Ladder Method can be used to find both the GCF and the LCM (see the instructional video below on how to use this tool).
The following clips will help you to review the concepts we discussed today in class:
| common_factors_and_multiples.jpg | |
| File Size: | 509 kb |
| File Type: | jpg |
| common_factors_and_multiples_part_2.jpg | |
| File Size: | 397 kb |
| File Type: | jpg |
Day #4 Calculating Powers
Reminders:
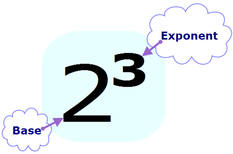
- A Power is a numerical expression that shows repeated multiplication. For example, the power 5² is a shorter way of writing 5×5.
- A power has a base and an exponent. The exponent tells the number of equal factors there are in a power.
- In the exponent 2³ the base is the 2 and the exponent is the 3. This could also be represented as 2×2×2=8.
- Most calculators have a yⁿ key (or something similar) to enter powers.
Reminders:
- A Power is a numerical expression that shows repeated multiplication. For example, the power 5² is a shorter way of writing 5×5.
- A power has a base and an exponent. The exponent tells the number of equal factors there are in a power.
- In the exponent 2³ the base is the 2 and the exponent is the 3. This could also be represented as 2×2×2=8.
- Most calculators have a yⁿ key (or something similar) to enter powers.
| calculating_powers_part_1.jpg | |
| File Size: | 449 kb |
| File Type: | jpg |
| calculating_powers_part_2.jpg | |
| File Size: | 439 kb |
| File Type: | jpg |
Day 5 EXPANDED FORM and SCIENTIFIC NOTATION
Sept. Activity Sheet (see file below)
Reminders:
- Standard Form (or Standard Notation) is the manner in which numbers are normally written Ex. 187
- Expanded Form is a way to break up a number to show how much each digit in the number represents. In other words, expanded form is the method of pulling a number apart and expressing it as a sum of the values of each digit.
Example, the expanded form of the number 543 is 500 + 40 + 3.
- Scientific Notation is a method of expressingnumbers in terms of a decimal number between 1 and 10 multiplied by a power of 10. The scientific notation for 10,492, for example, is 1.0492 × 10⁴.
Sept. Activity Sheet (see file below)
Reminders:
- Standard Form (or Standard Notation) is the manner in which numbers are normally written Ex. 187
- Expanded Form is a way to break up a number to show how much each digit in the number represents. In other words, expanded form is the method of pulling a number apart and expressing it as a sum of the values of each digit.
Example, the expanded form of the number 543 is 500 + 40 + 3.
- Scientific Notation is a method of expressingnumbers in terms of a decimal number between 1 and 10 multiplied by a power of 10. The scientific notation for 10,492, for example, is 1.0492 × 10⁴.
| expanded_form_and_scientific_notation.pdf | |
| File Size: | 998 kb |
| File Type: | |
Day 6 MID UNIT REVIEW
Sept. Textbook page 25 #1, 3, 4(a,b), 6 ,8, 10
In preparation for a review quiz on the first 5 math concepts covered in this unit, the students worked on the following practice questions: Mid Unit Review textbook page 25 #1, 3, 4(a,b), 6, 8, 10
Due: Sept. 17
Day 7 CORRECTION OF MID UNIT REVIEW
Sept.
We spent the time in math today correcting yesterdays review questions in preparation for tomorrows first quiz.
We spent the time in math today correcting yesterdays review questions in preparation for tomorrows first quiz.
MID UNIT QUIZ
The students wrote their first quiz..
Day 9 SQUARE ROOTS
Sept. Complete Square Root Activity Page 8 (see file below)
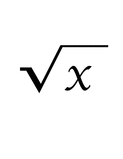
SQUARE ROOT KEY
Reminders:
Square Root - a number that when multiplied by itself equals a given number. Example, the square root of 25 is 5, because 5x5 = 25.
Any square root answer that has a whole number answer is considered to be a "perfect square." Therefore, 25 is a perfect square.
Non-Perfect Square - When you find the square root of the number, it does not give you a whole number answer. Example, the square root of 6 = 2.449
Estimate - A close guess of the actual value, usually with some thought or calculation involved.
The following video will help you to visualize Perfect Squares and Square Roots:
Square Root - a number that when multiplied by itself equals a given number. Example, the square root of 25 is 5, because 5x5 = 25.
Any square root answer that has a whole number answer is considered to be a "perfect square." Therefore, 25 is a perfect square.
Non-Perfect Square - When you find the square root of the number, it does not give you a whole number answer. Example, the square root of 6 = 2.449
Estimate - A close guess of the actual value, usually with some thought or calculation involved.
The following video will help you to visualize Perfect Squares and Square Roots:
To round the answer to a non-perfect square, follow this method:
| square_roots_activity_page.pdf | |
| File Size: | 910 kb |
| File Type: | |
Day 10 ORDER OF OPERATIONS WITH EXPONENTS
Reminders:
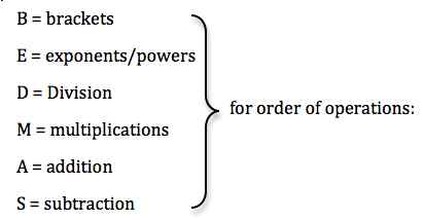
Order of Operations - These are the rules that states which calculation is to be performed first in an expression.
They order is as follows:
(1) Do all calculations inside brackets first
(2) Then complete all calculation that involve exponents
(3) Then complete all multiplication and division calculations as they appear from left to right
(4) Lastly do all of the addition and subtraction calculations as they appear from left to right
Order of Operations - These are the rules that states which calculation is to be performed first in an expression.
They order is as follows:
(1) Do all calculations inside brackets first
(2) Then complete all calculation that involve exponents
(3) Then complete all multiplication and division calculations as they appear from left to right
(4) Lastly do all of the addition and subtraction calculations as they appear from left to right
| order_of_operations.pdf | |
| File Size: | 1706 kb |
| File Type: | |
Day 11 ORDER OF OPERATIONS WITH EXPONENTS PART II
As a follow-up to the last lesson, the students will complete a second day on order of operations with exponents as a means of solidifying their retention.
Day 12 CHAPTER REVIEW
Sept. page 41 #1-4, 6-13
Today the students will complete a review of all the concepts covered during the unit on Number Relationships. The unit test is scheduled for Tuesday, September 27th.
Today the students will complete a review of all the concepts covered during the unit on Number Relationships. The unit test is scheduled for Tuesday, September 27th.
Day 13 UNIT TEST