Day 1 Coordinates of Points on a Grid
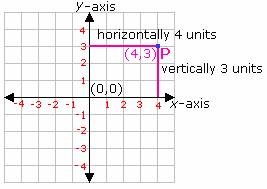
Cartesian coordinates can be used to pinpoint where you are on a map or graph. A Cartesian Coordinate plane is essentially two number lines (one vertical and one horizontal) that cross at a fixed point called the "origin" - marked on the grid as point (0,0). Each of the individual number lines is called an axis.
Using Cartesian Coordinates you can mark a point on a graph by indicating how far to the left or right and up and down it is from the origin (0,0).
The coordinates are always written in a certain order:
Cartesian coordinates can be used to pinpoint where you are on a map or graph. A Cartesian Coordinate plane is essentially two number lines (one vertical and one horizontal) that cross at a fixed point called the "origin" - marked on the grid as point (0,0). Each of the individual number lines is called an axis.
Using Cartesian Coordinates you can mark a point on a graph by indicating how far to the left or right and up and down it is from the origin (0,0).
The coordinates are always written in a certain order:
- the horizontal (left-right) distance is called the X co-ordinate and is always written first,
- the vertical distance (up-down) distance is called the Y co-ordinate and is always written second.
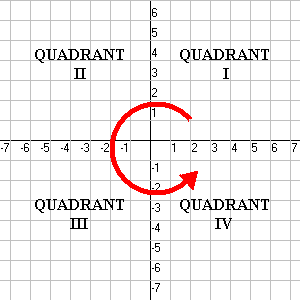
The Cartesian plane is divided into four quadrants. These are numbered from 1 through 4, starting with the upper right and going around counterclockwise (see diagram below).
|
|
In Quadrant I, both the x– and y-coordinates are positive; in Quadrant II, the x-coordinate is negative, but the y-coordinate is positive; in Quadrant III both are negative; and in Quadrant IV x is positive but y is negative.
Points which lie on an axis (i.e., which have at least one coordinate equal to 0) are said not to be in any quadrant. Coordinates of the form (x, 0) lie on the horizontal x-axis, and coordinates of the form (0, y) lie on the vertical y-axis. The video (to the left) highlights the basics of the Cartesian Co-ordinate Plane, key vocabulary and explains quadrants and how to plot co-ordinates. |
Translations on a Co-ordinate Plane
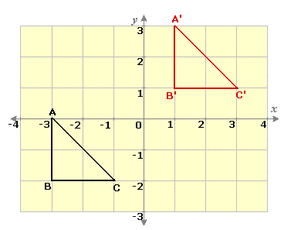
A translation is a transformation of the plane that slides every point of a figure the same distance in the same direction. When a figure is translated it remains the same or congruent.
When we TRANSLATE a figure in the coordinate plane, we add the translation amount to all the ordered pairs that make up the figure. Remember to:
A translation is a transformation of the plane that slides every point of a figure the same distance in the same direction. When a figure is translated it remains the same or congruent.
When we TRANSLATE a figure in the coordinate plane, we add the translation amount to all the ordered pairs that make up the figure. Remember to:
- Name the ordered pairs of all the points that make up the figure
- Add the x-value of the translation to all the x-coordinates
- Add the y-value of the translation to all the y-coordinates
- Rewrite all the new ordered pairs and sketch the new figure
|
Translation Vector
A Translation Vector is a vector that gives the length and direction of a particular translation. Vectors in the Cartesian plane can be written [x,y] which means a translation of x units horizontally and y units vertically. Note: Square brackets [ ] are used for translation vectors to show the difference between them and ordered pairs. |
|
Reflections in the Co-ordinate Plane
When you look in the mirror, you see your reflection. In math, you can create mirror images of figures by reflecting them over a given line.
When a figure is reflected over a given line, the resulting figure is called its Reflection. The reflection is the mirror image of the original figure and the line of reflection is the mirror. If your were able to fold the picture along the line of reflection, the original picture and its reflection would align perfectly.
When you look in the mirror, you see your reflection. In math, you can create mirror images of figures by reflecting them over a given line.
When a figure is reflected over a given line, the resulting figure is called its Reflection. The reflection is the mirror image of the original figure and the line of reflection is the mirror. If your were able to fold the picture along the line of reflection, the original picture and its reflection would align perfectly.
|
|
|
In the second video, ignore the section on "Reflecting in a Segment" (from the 4:40 to 6:46). Although interesting, and something that you will need to know eventually, you will not be tested on that concept in grade 8 this year. The remainder of the video is very helpful though.
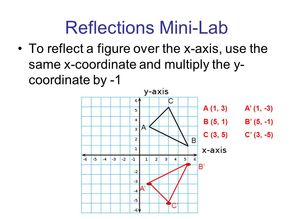
Review: (you can also view these rules in the image from up above)
Reflection in the x-axis is (x,y) → (x,-y)
Reflection in the y-axis is (x,y) → (-x,y)
Reflection in a diagonal line through (1,1) or y=x is (x,y)→(y,x)
Reflection in a diagonal line through (-1,1) or y=-x is (x,y)→(−y,−x)
Review: (you can also view these rules in the image from up above)
Reflection in the x-axis is (x,y) → (x,-y)
Reflection in the y-axis is (x,y) → (-x,y)
Reflection in a diagonal line through (1,1) or y=x is (x,y)→(y,x)
Reflection in a diagonal line through (-1,1) or y=-x is (x,y)→(−y,−x)
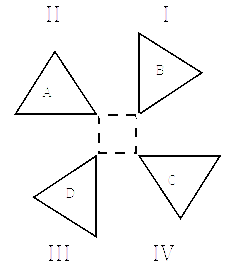
Rotations in the Co-ordinate Plane
When a figure is turned about a given point, the transformation is called a rotation. The figure is rotated counterclockwise or clockwise about a fixed point. The fixed point is called the "center of rotation."
Note: For grade , the center of rotation will always be the origin (0,0).
When a figure is turned about a given point, the transformation is called a rotation. The figure is rotated counterclockwise or clockwise about a fixed point. The fixed point is called the "center of rotation."
Note: For grade , the center of rotation will always be the origin (0,0).
Rules of Rotation
As the above left image and the below left video display there are rules for rotation in a:
Clockwise Direction (CW)
As the above left image and the below left video display there are rules for rotation in a:
Clockwise Direction (CW)
- The rule for a rotation by 90° about the origin is (x,y)→(y, -x)
- The rule for a rotation by 180° about the origin is (x,y)→(−x,−y)
- The rule for a rotation by 270° about the origin is (x,y)→(-y, x)
- The rule for a rotation by 90° about the origin is (x,y)→(-y, x)
- The rule for a rotation by 180° about the origin is (x,y)→(−x,−y)
- The rule for a rotation by 270° about the origin is (x,y)→(y, -x)
|
|
|
|
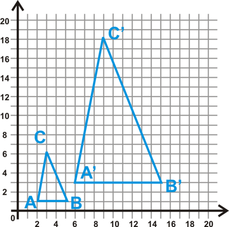
Dilations in the Co-ordinate Plane
A dilation makes a figure larger or smaller, but has the same shape as the original (see figure to the right). In other words, the dilation is similar, but not the exact same as the original. All dilations have a center and a scale factor. The center is the point of reference for the dilation (like the vanishing point in a perspective drawing) and scale factor tells us how much the figure stretches or shrinks. Note: in geometry scale factor is often symbolized using the letter K or point A (x,y)→ A′(Kx, Ky) if K is greater than 1 the original object will stretch and if K is less than 1 the original object will shrink. To dilate something in the coordinate plane, multiply each coordinate by the scale factor (K). This is called mapping. If the scale factor is 3 (K=3), then simply multiply each of the original coordinates by 3. For example, if the original coordinates of △ABC are A (2,1), B (5,1) and C (3,6), then the coordinates of △A′B′C′ are: A′ → (2x3, 1,3) or (6,3), B′ → (5x3, 1x3) or (15,3) and C′ → (3x3, 6x3) or (9,18). The image will be 3 times larger than the original object. If the scale factor is 0.5, then simply multiply each of the original coordinates by 0.5. The image will be half the size of the original shape. |
|
|
|
Review of Unit
|
|
|