PATTERNS AND RELATIONSHIPS
Day #1 THE FIBONACCI SEQUENCE
About Fibonacci The ManHis real name was Leonardo Pisano Bogollo, and he lived between 1170 and 1250 in Italy.
"Fibonacci" was his nickname, which roughly means "Son of Bonacci".
As well as being famous for the Fibonacci Sequence, he helped spread Hindu-Arabic Numerals (like our present numbers 0,1,2,3,4,5,6,7,8,9) through Europe in place of Roman Numerals (I, II, III, IV, V, etc). That has saved us all a lot of trouble! Thank you Leonardo.
History
Fibonacci was not the first to know about the sequence, it was known in India hundreds of years before!
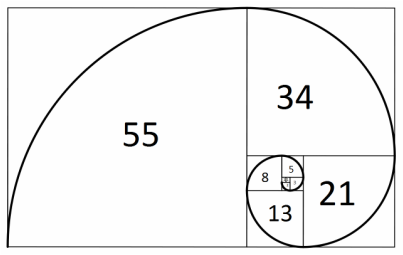
The Fibonacci Sequence
The Fibonacci Sequence is the series of numbers:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
The next number is found by adding up the two numbers before it.
Here is a longer list:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ...
And here is a surprise. When we take any two successive (one after the other) Fibonacci Numbers, their ratio is very close to the Golden Ratio"φ" which is approximately 1.618034...
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
AB B / A
23 1.5
35 1.666666666...
58 1.6
813 1.625
...... ...
144233 1.618055556...
233377 1.618025751.
About Fibonacci The ManHis real name was Leonardo Pisano Bogollo, and he lived between 1170 and 1250 in Italy.
"Fibonacci" was his nickname, which roughly means "Son of Bonacci".
As well as being famous for the Fibonacci Sequence, he helped spread Hindu-Arabic Numerals (like our present numbers 0,1,2,3,4,5,6,7,8,9) through Europe in place of Roman Numerals (I, II, III, IV, V, etc). That has saved us all a lot of trouble! Thank you Leonardo.
History
Fibonacci was not the first to know about the sequence, it was known in India hundreds of years before!
The Fibonacci Sequence
The Fibonacci Sequence is the series of numbers:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
The next number is found by adding up the two numbers before it.
- The 2 is found by adding the two numbers before it (1+1)
- Similarly, the 3 is found by adding the two numbers before it (1+2),
- And the 5 is (2+3),
- and so on!
Here is a longer list:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ...
And here is a surprise. When we take any two successive (one after the other) Fibonacci Numbers, their ratio is very close to the Golden Ratio"φ" which is approximately 1.618034...
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
AB B / A
23 1.5
35 1.666666666...
58 1.6
813 1.625
...... ...
144233 1.618055556...
233377 1.618025751.
Day #2 EXPLORING RELATIONSHIP
The ability to recognize abstract patterns in number sequences is a skill that lays the foundation for data analysis abilities later in math. In grade eight we focus on creating algebraic expressions from these sequences. Today we will focus on identifying patterns in sets of numbers, predicting numbers that occur later within the sequence and expressing the pattern in words.
Check this weblink out to find a great module of the concept of patterns in sequences: http://bit.ly/skw56X
The following clips provide a good overview of what we will discuss in class:
Check this weblink out to find a great module of the concept of patterns in sequences: http://bit.ly/skw56X
The following clips provide a good overview of what we will discuss in class:
Mathematics is especially useful when it helps you predict, and number patterns are all about prediction. What will the 50th number of a pattern be? How many cupcakes would we need if we gave a party for the town instead of just our class? Working with number patterns leads directly to the concept of functions in mathematics: a formal description of the relationships among different quantities.
Recognizing number patterns is also an important problem-solving skill. If you see a pattern when you look systematically at specific examples, you can use that pattern to generalize what you see into a broader solution to a problem.
Reminders:
Arithmetic Sequence: is a sequence of numbers that has a constant difference between every two consecutive terms. In other words, arithmetic sequence is a sequence of numbers in which each term except the first term is the result of adding the same number, called the common difference, to the term before it.
Geometric Sequence : is a sequence of numbers that has a constant multiple between every two consecutive terms. In other words, the next term originates by multiplying the predecessor by a constant.
Fibonacci Sequence: is a sequence of numbers in which the next term originates by the addition of the previous two. This sequence is called the "Golden Ratio", and many believe it is proof of the fingerprint of God within creation (including our own bodies). Watch the following clips to see how often the "Fibonacci Spiral" reveals itself in nature and you begin to see there is something special about this pattern:
Recognizing number patterns is also an important problem-solving skill. If you see a pattern when you look systematically at specific examples, you can use that pattern to generalize what you see into a broader solution to a problem.
Reminders:
Arithmetic Sequence: is a sequence of numbers that has a constant difference between every two consecutive terms. In other words, arithmetic sequence is a sequence of numbers in which each term except the first term is the result of adding the same number, called the common difference, to the term before it.
Geometric Sequence : is a sequence of numbers that has a constant multiple between every two consecutive terms. In other words, the next term originates by multiplying the predecessor by a constant.
Fibonacci Sequence: is a sequence of numbers in which the next term originates by the addition of the previous two. This sequence is called the "Golden Ratio", and many believe it is proof of the fingerprint of God within creation (including our own bodies). Watch the following clips to see how often the "Fibonacci Spiral" reveals itself in nature and you begin to see there is something special about this pattern:
| number_patterns_activity_sheet_1.jpg | |
| File Size: | 199 kb |
| File Type: | jpg |
| number_patterns_activity_sheet_2.jpg | |
| File Size: | 187 kb |
| File Type: | jpg |
Tonight the students are to complete the 2 Number Pattern Activity Sheets from above.
Due: Wednesday, Oct. 26th
Due: Wednesday, Oct. 26th
Day #3 CREATING PATTERN RULES FROM MODELS
Reminders:
a) Models/ Manipulatives: To help visualize what a pattern looks like it may be helpful to use concrete materials to represent the pattern. Common materials used to design a pattern would include things like stir sticks, blocks and straws.
b) Variable: A letter or symbol such as a, b or n, that represents a number that changes in an algebraic expression.
c) Constant: A number in an algebraic expression that is fixed (stays the same). It is either added or subtracted within an algebraic equation. In order to find constant we must find the "zero" term (see below).
d) Multiplier: The number in an algebraic expression that is the difference between adjacent terms.
e) Algebraic Rule/Expression: A math sentence that contains one or more numbers, one or more variables, and one or more arithmetic operations. In the sentence, 5a + 3, the letter a is the variable, the numbers 5 is the multiplier and the 3 is the constant.
Example:
In the sequence 5, 9, 13, 17, 21,...
We can find the multiplier by subtracting adjacent terms (9-5=4, 13-9=4, 17-13=4, 21-17=4 etc.)
Therefore, the number 4 is the multiplier.
In this sequence, the 5 is considered to be the first term, the 9 is the second term, the 13 is the third term, etc.
To find the zero term we simply subtract the first term by the multiplier. In this case 5-4=1.
Therefore, 1 is the zero term constant.
The variable is the number that we use to represent the changing number in the expression. In this case the changing number is the term number. We can select any letter in the alphabet to represent the variable (n is often used as the variable in algebra).
Therefore, the algebraic expression for this sequence is 4n + 1 (4 is the multiplier, n is the variable, and +1 is the constant).
The following clips show how algebraic rules can be created using modelling sticks. The number pattern in the first clip may seem obvious, however creating the subsequent algebraic expression that corresponds to the number pattern requires some practice and a keen eye.
Reminders:
a) Models/ Manipulatives: To help visualize what a pattern looks like it may be helpful to use concrete materials to represent the pattern. Common materials used to design a pattern would include things like stir sticks, blocks and straws.
b) Variable: A letter or symbol such as a, b or n, that represents a number that changes in an algebraic expression.
c) Constant: A number in an algebraic expression that is fixed (stays the same). It is either added or subtracted within an algebraic equation. In order to find constant we must find the "zero" term (see below).
d) Multiplier: The number in an algebraic expression that is the difference between adjacent terms.
e) Algebraic Rule/Expression: A math sentence that contains one or more numbers, one or more variables, and one or more arithmetic operations. In the sentence, 5a + 3, the letter a is the variable, the numbers 5 is the multiplier and the 3 is the constant.
Example:
In the sequence 5, 9, 13, 17, 21,...
We can find the multiplier by subtracting adjacent terms (9-5=4, 13-9=4, 17-13=4, 21-17=4 etc.)
Therefore, the number 4 is the multiplier.
In this sequence, the 5 is considered to be the first term, the 9 is the second term, the 13 is the third term, etc.
To find the zero term we simply subtract the first term by the multiplier. In this case 5-4=1.
Therefore, 1 is the zero term constant.
The variable is the number that we use to represent the changing number in the expression. In this case the changing number is the term number. We can select any letter in the alphabet to represent the variable (n is often used as the variable in algebra).
Therefore, the algebraic expression for this sequence is 4n + 1 (4 is the multiplier, n is the variable, and +1 is the constant).
The following clips show how algebraic rules can be created using modelling sticks. The number pattern in the first clip may seem obvious, however creating the subsequent algebraic expression that corresponds to the number pattern requires some practice and a keen eye.
Today students used models to identify patterns and create algebraic expressions.
Due: Oct. 31st
Due: Oct. 31st
Day #4 USING A T-CHART TO FIND THE Nth TERM OF A SEQUENCE
Reminders:
nth term: is the general expression used to find the value of any dependent variable in a sequence
T Chart: is an organizational tool that is designed to place information into two separate columns. The purpose of the two columns is to enable group participants to better compare various ideas and, in the end, make better decisions.
Table of Values: is a list of numbers that are used to substitute one variable, such as within an equation of a line and other functions, to find the value of the other variable, or missing number.
Independent Variable: is the first number in a table of values chosen to find the second value. It may also be referred to as the term number, the figure number or the "x" coordinate. It is independently chosen for the equation.
Dependent Variable: is the second number in a table of values. It is found as the solution of the algebraic expression. It may also be referred to as the term value, the figure value or the "y" coordinate. The dependent variable relies upon the chosen value of the independent variable.
Below is an example of a Table of Values set up in a T chart organizer.
Reminders:
nth term: is the general expression used to find the value of any dependent variable in a sequence
T Chart: is an organizational tool that is designed to place information into two separate columns. The purpose of the two columns is to enable group participants to better compare various ideas and, in the end, make better decisions.
Table of Values: is a list of numbers that are used to substitute one variable, such as within an equation of a line and other functions, to find the value of the other variable, or missing number.
Independent Variable: is the first number in a table of values chosen to find the second value. It may also be referred to as the term number, the figure number or the "x" coordinate. It is independently chosen for the equation.
Dependent Variable: is the second number in a table of values. It is found as the solution of the algebraic expression. It may also be referred to as the term value, the figure value or the "y" coordinate. The dependent variable relies upon the chosen value of the independent variable.
Below is an example of a Table of Values set up in a T chart organizer.
Students may use a T chart to organize a sequence of numbers to find the nth term (otherwise known as the algebraic expression). Once this is found, they merely have to substitute a value into the independent variable (x coordinate) to find the subsequent value of the dependent variable (y coordinate).
Due: Nov. 1st
Day 4 MID CHAPTER REVIEW
Day 5 MID CHAPTER QUIZ
Day #6 GRAPHING LINEAR SEQUENCES
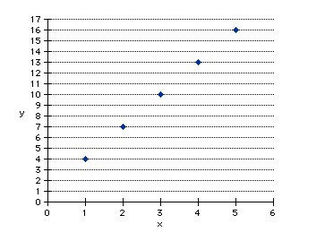
Graphing Linear Sequences
A graph is often used in math to display a sequence of numbers and then make predictions about the sequence using the “slope” of the graphed line.
The “slope of the line” refers to the angle that the line goes up (or down).
The following are things to consider when graphing a sequence:
· The Independent Variable (aka the Term Number) is always graphed along the x-axis.
· The Dependent Variable (aka the Term Value) is always graphed along the y-axis.
· The slope of the line will always cross the y-axis at the zero term. This will display the constant of the algebraic expression.
A graph is often used in math to display a sequence of numbers and then make predictions about the sequence using the “slope” of the graphed line.
The “slope of the line” refers to the angle that the line goes up (or down).
The following are things to consider when graphing a sequence:
· The Independent Variable (aka the Term Number) is always graphed along the x-axis.
· The Dependent Variable (aka the Term Value) is always graphed along the y-axis.
· The slope of the line will always cross the y-axis at the zero term. This will display the constant of the algebraic expression.