INTEGER OPERATIONS
Day 1 THE ZERO PRINCIPLE
A positive integer is any whole number above zero (or to the right of zero on a number line). Example, positive 3 can be written as +3 or simply 3.
A negative integer is any whole number that is below zero (or to the left of zero on a number line). Example, negative 6 can be written as -6.
Any two integers that have the same number but opposite signs are called opposite integers as they are equadistant from zero on a number line. Example, +7 and -7 are opposite to one another.
Integer tiles are a math manipulative that can be used to help solve simple addition and subtraction questions for students who are kinesthetic and visual learners. When using integer tiles we can use temperatures as a guide. The red tiles (hot) are considered positive numbers and the blue tiles (cold) are considered negative numbes.
The Zero Principle When adding integers we can use this principle to arrive at the final answer. By pairing up opposite coloured tiles we can cancel them out as one red tile (representing +1) and one blue tile (representing -1) will take us back to zero tiles. The number and colour of tiles left over after the tiles have been paired will be the final answer.
For example, if I have 6 red tiles and 4 blue tiles, I can pair up 4 of the red with 4 of the blue. They will cancel each other out. I am left with 2 red tiles, so my final answer is +2.
When subtracting, we include both colours to represent the number that is being subtracted.
For example, (+6) - (-2). To solve this using integer tiles I would represent the +6 using 6 red tiles. To represent the (-2) I would include two red tiles and two blue tiles (4 tiles altogether). I then subtract the two negative (blue) tiles and count up how many tiles I have left. In this case I would have 8 red tiles, so my answer would be +8.
For example, if I have 6 red tiles and 4 blue tiles, I can pair up 4 of the red with 4 of the blue. They will cancel each other out. I am left with 2 red tiles, so my final answer is +2.
When subtracting, we include both colours to represent the number that is being subtracted.
For example, (+6) - (-2). To solve this using integer tiles I would represent the +6 using 6 red tiles. To represent the (-2) I would include two red tiles and two blue tiles (4 tiles altogether). I then subtract the two negative (blue) tiles and count up how many tiles I have left. In this case I would have 8 red tiles, so my answer would be +8.
Day 2 ADDING AND SUBTRACTING INTEGERS

Subtracting Integers
Addition
When adding integers it is often handy to consider money. Positive integers reflect money you have earned, whereas negative integers reflect money you owe.
Example 1, (+10) + (-3) = (+7)
In this example, the +10 reflects $10 I have earned. The (-3) indicates $3 I owe. Therefore, if I pay the person back what I owe them, I will have $7 remaining.
Example 2, (-10) + (-3) = (-13)
In this example, you owe someone $10 and someone else $3. Therefore your total debt is $13 or (-13).
Subtracting
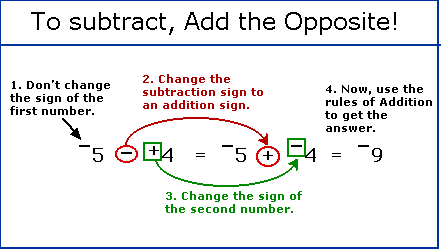
When subtracting integers, remember this one simplerule: "Add the opposite of the second integer."
Study the example in the picture above to see how to change a subtraction problem into addition.
(1) Keep the sign of the first integer the way it appeared in the original question.
(2) Change the subtraction operation to addition.
(3) Change the sign of the second integer to it's opposite.
(4) Now go back and use the addition rules given above.
When adding integers it is often handy to consider money. Positive integers reflect money you have earned, whereas negative integers reflect money you owe.
Example 1, (+10) + (-3) = (+7)
In this example, the +10 reflects $10 I have earned. The (-3) indicates $3 I owe. Therefore, if I pay the person back what I owe them, I will have $7 remaining.
Example 2, (-10) + (-3) = (-13)
In this example, you owe someone $10 and someone else $3. Therefore your total debt is $13 or (-13).
Subtracting
When subtracting integers, remember this one simplerule: "Add the opposite of the second integer."
Study the example in the picture above to see how to change a subtraction problem into addition.
(1) Keep the sign of the first integer the way it appeared in the original question.
(2) Change the subtraction operation to addition.
(3) Change the sign of the second integer to it's opposite.
(4) Now go back and use the addition rules given above.
The following video provides several different options for adding and subtracting integers. The method we looked at in school today for subtracting integers can be found at the 5 minute mark. Check out the other methods to find out what is most comfortable for you personally.
Day 3 MULTIPLYING INTEGERS
Multiplying integers is just like the multiplication of whole numbers, except that with integers, you have to keep tract of your signs.
Recall that 6 + 6 + 6 = 6 × 3
Instead of adding 6 three times, you can multiply 6 by 3 and get 18, the same answer.
Similarly, 6 + 6 + 6 + 6 + 6 + 6 + 6 = 6 × 7 = 42
**In algebra, 6 × 7 can be written as (6)(7). Notice that the lack of a mathematical operation between the parentheses indicate that these integers are to be multiplied.
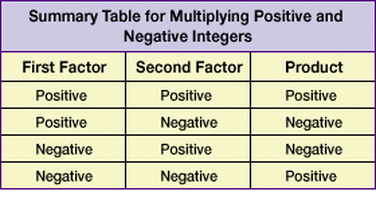
As the above table shows, the rules for multiplying integers are as follows:
The product of two numbers with the same signs will be positive.
The product of two numbers with different signs will be negative.
Recall that 6 + 6 + 6 = 6 × 3
Instead of adding 6 three times, you can multiply 6 by 3 and get 18, the same answer.
Similarly, 6 + 6 + 6 + 6 + 6 + 6 + 6 = 6 × 7 = 42
**In algebra, 6 × 7 can be written as (6)(7). Notice that the lack of a mathematical operation between the parentheses indicate that these integers are to be multiplied.
As the above table shows, the rules for multiplying integers are as follows:
The product of two numbers with the same signs will be positive.
The product of two numbers with different signs will be negative.
Day 4 MID CHAPTER REVIEW

page 186 #1-7, 10-16
Due: Monday, January 16th
Due: Monday, January 16th
Day 5 Dividing Integers

Division of Negative and Positive Integers
The division of Integers is similar to division of whole numbers (both positive) except the sign of the quotient (answer to a division question) needs to be determined.
If both the dividend and divisor are positive, the quotient will be positive. (+16) ÷ (+4) = +4
If both the dividend and divisor are negative, the quotient will be positive. (-16) ÷ (-4) = +4
If only one of the dividend or divisor is negative, the quotient will be negative.
(+16) ÷ (-4) = -4 or (-16) ÷ (+4) = -4
***If the signs are the same the quotient will be positive, if they are different, the quotient will be negative.
The division of Integers is similar to division of whole numbers (both positive) except the sign of the quotient (answer to a division question) needs to be determined.
If both the dividend and divisor are positive, the quotient will be positive. (+16) ÷ (+4) = +4
If both the dividend and divisor are negative, the quotient will be positive. (-16) ÷ (-4) = +4
If only one of the dividend or divisor is negative, the quotient will be negative.
(+16) ÷ (-4) = -4 or (-16) ÷ (+4) = -4
***If the signs are the same the quotient will be positive, if they are different, the quotient will be negative.
This video is less formal, but still gets the point across:
Day 6 Order of Operations With Integers

What is PEMDAS?
PEMDAS is an acronym for the words Parenthesis Exponents Multiplication Division Addition Subtraction. Given two or more operations in a single expression, the order of the letters in PEMDAS tells you what to calculate first second, third, etc., until the calculation is complete. If there are grouping symbols in the expression, PEMDAS tells you to calculate within the grouping symbols first.
****When solving a problem involving more than one operation it is important to remember the acronym PEMDAS (or BEDMAS).
Note: Parentheses and Brackets mean the same thing
A Useful Mnemonic
The letters PEMDAS and the words Parenthesis Exponents Multiplication Division Addition Subtraction may not be very meaningful for someone trying to remember this order, so a phrase has also been attached with the letters in PEMDAS--Please Excuse My Dear Aunt Sally. If you can remember this phrase, then it may be easier to remember the order of operations given in PEMDAS.
****It is important to work vertically along the page to solve these types of questions and always "bring down" the numbers you have yet to calculate to the line below the operation you just dealt with.
How to Use PEMDAS to Solve Order of Operation Questions
PEMDAS is an acronym for the words Parenthesis Exponents Multiplication Division Addition Subtraction. Given two or more operations in a single expression, the order of the letters in PEMDAS tells you what to calculate first second, third, etc., until the calculation is complete. If there are grouping symbols in the expression, PEMDAS tells you to calculate within the grouping symbols first.
****When solving a problem involving more than one operation it is important to remember the acronym PEMDAS (or BEDMAS).
Note: Parentheses and Brackets mean the same thing
A Useful Mnemonic
The letters PEMDAS and the words Parenthesis Exponents Multiplication Division Addition Subtraction may not be very meaningful for someone trying to remember this order, so a phrase has also been attached with the letters in PEMDAS--Please Excuse My Dear Aunt Sally. If you can remember this phrase, then it may be easier to remember the order of operations given in PEMDAS.
****It is important to work vertically along the page to solve these types of questions and always "bring down" the numbers you have yet to calculate to the line below the operation you just dealt with.
How to Use PEMDAS to Solve Order of Operation Questions
Solving Problems that Include Both Square and Round Brackets
For certain order of operation questions, the use of square brackets will appear. These are used to distinguish when there is more than one set of parentheses (brackets) surrounding operations within the same question. See the example video below:
For certain order of operation questions, the use of square brackets will appear. These are used to distinguish when there is more than one set of parentheses (brackets) surrounding operations within the same question. See the example video below: