UNIT # 4
MEASUREMENT OF CIRCLES
Day 1 EXPLORING CIRCLES
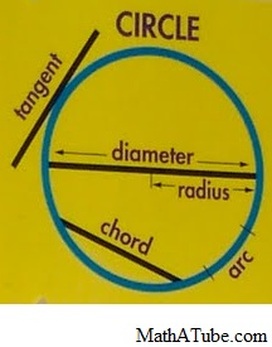
As an introduction to solving problems related to circles, students will construct circles and explore measurements related to radius, diameter and circumference.
Radius - a straight line that extends from the centre of a circle to the outside edge. It is equal to half the distance across a circle.
Diameter - a straight line that extends from one edge of a circle, passes through the center of the circle and touches the other side. It is twice the length of the radius.
Circumference - is the distance around the outside edge of a circle. It is about 3 times longer than the diameter.
Chord - a straight line that joins any two points on the circumference of a circle.
Arc - a section of the circumference of a circle that lies between two ends of a chord (each chord creates two arcs).
Radius - a straight line that extends from the centre of a circle to the outside edge. It is equal to half the distance across a circle.
Diameter - a straight line that extends from one edge of a circle, passes through the center of the circle and touches the other side. It is twice the length of the radius.
Circumference - is the distance around the outside edge of a circle. It is about 3 times longer than the diameter.
Chord - a straight line that joins any two points on the circumference of a circle.
Arc - a section of the circumference of a circle that lies between two ends of a chord (each chord creates two arcs).
Day 2 CALCULATING CIRCUMFERENCE
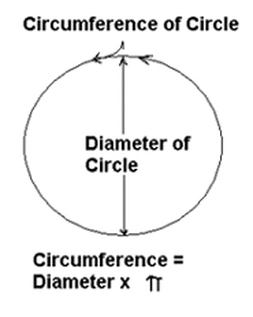
Yesterday we learned that the circumference of a circle is approximately three times its diameter. When finding the approximate answer to a question we use the symbol (≈) to indicate that the answer is close to but not exactly the correct answer.
Often measuring the circumference is impractical or a more exact formula than "about 3 times" is needed.
Today students will learn the exact formula for calculating the distance around a circle (circumference) using the constant Pi
(π = 3.14).
For more information on the history and uses of π
in math check out the following weblink: http://bit.ly/brYCsl
The formula for estimating the approximate length of the circumference of a circle is C = 3d where C stands for circumference, and d stands for diameter
The formula for calculating the exact length of the circumference of a circle is C = πd, where C stands for circumference, π is the symbol for 3.14 and d stands for diameter.
** When only the radius is known, you need to multiply it by 2 (2r = d) to find the diameter.
For an funny (but informative) song to help to remember circumference, π and diameter check out this link to teachertube that changes the lyrics of the Tommy Twotone song 86953o9 to 3.14159 http://bit.ly/vWeyfR
Due: Dec. 13th
Often measuring the circumference is impractical or a more exact formula than "about 3 times" is needed.
Today students will learn the exact formula for calculating the distance around a circle (circumference) using the constant Pi
(π = 3.14).
For more information on the history and uses of π
in math check out the following weblink: http://bit.ly/brYCsl
The formula for estimating the approximate length of the circumference of a circle is C = 3d where C stands for circumference, and d stands for diameter
The formula for calculating the exact length of the circumference of a circle is C = πd, where C stands for circumference, π is the symbol for 3.14 and d stands for diameter.
** When only the radius is known, you need to multiply it by 2 (2r = d) to find the diameter.
For an funny (but informative) song to help to remember circumference, π and diameter check out this link to teachertube that changes the lyrics of the Tommy Twotone song 86953o9 to 3.14159 http://bit.ly/vWeyfR
Due: Dec. 13th
Day 3 MID-CHAPTER REVIEW
page 160-161 #1-7
Reminders
Don't forget to use approximately equal to (≈) and the number 3 when estimating.
Don't forget to use equal to and Pi (π) when calculating exact answers.
Day 4 CALCULATING AREA
page 166-167 #4-9
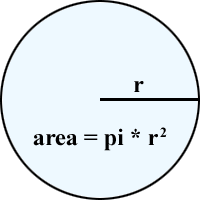
The area of a shape refers to how much space it occupies.
When estimating the area of a circle we use the formula: A = 3r²
When calculating the area of a circle we use the formula: A = πr²
**1) Remember to always use square units in the answer for area questions.
**2) If the question only provides the diameter, you need to remember to divide it in two to find the radius.
When estimating the area of a circle we use the formula: A = 3r²
When calculating the area of a circle we use the formula: A = πr²
**1) Remember to always use square units in the answer for area questions.
**2) If the question only provides the diameter, you need to remember to divide it in two to find the radius.
Day 5 SOLVE PROBLEMS BY WORKING BACKWARD
Dec. 19th page 170 #5-7, 10-12
Today students will use a four step problem-solving plan to implement the strategy of working backwards, starting with values they know to solve for the values they do not know. In order to work backward to solve circle measurement problems, students must have a good understanding of the formulas for finding circumference and area of a circle. The students must also recognize the relationships of radius, diameter, circumference and/or area within the formula.
When solving problems working backwards it is helpful if students follow a plan. I encourage a four-step plan.
Step 1 - Read the question carefully and copy down the information that has been given.
If the circumference of a circle is given copy down the circumference formula (C = πd). If the area of a circle is given copy down the area formula (A = πr²).
Step 2 - Replace the symbols and variables in the formula with the known numbers from the question.
Step 3 - Group the numbers on one side of the equal sign and the variables (letters) on the other.
**When the number(s) move to the other side of the equal sign, the operation that is performed becomes opposite to what it was on the original side of the equation. In other words, if you multiplied a number on the right side of the equal sign, you will divide that number on the left side of the equal sign.
Step 4 - Solve the equation to find the unknown variable.
Example - A lawn sprinkler rotates and sprays water in a circle. It sprays an area of 283 m². What is the radius of the circle in which it sprays.
Step 1 - Copy down the information that has been given.
A = 283 m² π = 3.14 A = πr²
Step 2 -Replace the symbols and variables in the formula with the known numbers.
A = πr²
283 m² = (3.14) (r²)
Step 3 - Group the numbers on one side of the equal sign and the variables on the other.
A = πr²
283 m² = (3.14) (r²)
283 m² ÷ 3.14 = r²
Step 4 - Solve the equation to find the unknown variable
A = πr²
283 m² = (3.14) (r²)
283 m² ÷ 3.14 = r²
90.13 = r² ( Note: the opposite of squaring a number is finding the square root)
(square root of) 90.13 = r
8.49 m = r
The sprinkler rotates with a radius of 8.49m.
Day 6 CIRCLES REVIEW
page 174-175 #1-10
Remember
Read the question carefully and select the necessary formula.
Always write down the formula to start the solution to the problem.
Radius = 1/2 Diameter (r = 1/2d) or Diameter is double the radius (d = 2r)
Circumference Formula C = πd
Area of Circle Formula A = πr²
